Le résultat final est une petite fleur à poser sur la surface de l'eau dans un verre. Elle s'ouvre toute seule...
C'est un objet en 3 dimensions (3D) qui est en mouvement et donc une math'@ctivité mouvement.
Pour voir cette petite fleur de nénufar en action, regarder la vidéo ci-dessus.
Infos...
Une "petite fleur de nénufar"

L’explication du mouvement : Les fibres du papier étant cassées aux plis, l’eau va se glisser à ces endroits. Par capillarité(1), elle va gonfler les fibres aux plis et monter dans les pétales en les forçant à se redresser. La petite fleur de nénufar(2) s’ouvre.
Pour l’utiliser à nouveau, il faut la faire sécher. Plus la fleur aura été utilisée et plus son ouverture sera rapide. Une eau tiède accélère également l'ouverture de fleur.
(1) : « CAPILLARITÉ : n.f. Ensemble des phénomènes relatifs au comportement des liquides dans des tubes très fins et à toutes situations où une surface de séparation entre deux fluides (liquide –gaz, par ex.) rencontre une paroi solide. (La capillarité joue, par ex., un rôle dans la montée de la sève.) » Extrait du dictionnaire : Le petit Larousse.
Ne nombreux calculs mathématiques sont utilisés pour cette notion physique.
(2) : l'orthographe en "f" est recommandée par l'Académie Française dans son rapport de 1990 sur les rectifications orthographiques. Le mot est d'origine sémitique et même égyptienne, et en aucun cas grec, comme pourrait le faire croire l'orthographe "nénuphar".
Matériel nécessaire :
instruments de géométrie : compas et règle graduée ;
1 feuille A4 (épaisse 160g/m2) ;
ciseaux, crayon à papier, crayons à bille et feutres de couleur (dont rouge) ou peinture.
Programme de construction
(savoirs et savoir-faire mathématiques : directions (Nord-Sud-Est-Ouest), sens des aiguilles d’une montre, centre d’un cercle,
cercle, rayon, corde, point d’intersection entre deux cercles, point d’intersection entre un cercle et une droite, médiatrice d’un segment, cercles concentriques et rosace.)
 Construction du patron de la petite fleur de nénufar :
Construction du patron de la petite fleur de nénufar :
- placer un point O1 et tracer le cercle C1 de centre O1 et de rayon 3,5 cm ;
- tracer 6 arcs de cercles en reportant 6 fois le rayon sur le cercle C1 (le résultat est une rosace) ;
- nommer, dans l’ordre et dans le sens des aiguilles d’une montre, les points d’intersection entre C1 et ces arcs : A, B, C, D, E et F sachant que A est le point le plus à l’Est ;
- tracer la corde [AB] ;
- construire la médiatrice de [AB] et la nommer (d) ;
- placer G, le point d’intersection entre (d) et C1 ;
- reporter 5 fois le rayon [AB] sur C1 à partir du point G (sans tracer les arcs) ;
- nommer, dans l’ordre et dans le sens des aiguilles d’une montre, les points d’intersection entre C1 et ces rayons reportés : H, I, J, K et L ;
- tracer les cercles C2 et C3 concentriques de centre O1 et de rayon respectivement 2 cm et 1,5 cm ;
- placer les points d’intersection entre C2 et les arcs de cercle : 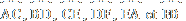 (il y en a 12) ;
(il y en a 12) ;
- nommer ces points : M (le point d’intersection entre 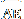 et C2 situé le plus au Sud) puis, dans l’ordre et dans le sens des aiguilles d’une montre, les points : N, O, P, Q, R, S, T, U, V, W et X ;
et C2 situé le plus au Sud) puis, dans l’ordre et dans le sens des aiguilles d’une montre, les points : N, O, P, Q, R, S, T, U, V, W et X ;
- tracer, en rouge, les segments : [MG], [GN], [OH], [HP],[QI],[IR],[SJ],[JT],[UK],[KV],[WL] et [LX] ;
- repasser, en rouge, les 12 arcs de cercles d’extrémités de départ les points A, B, C, D, E et F et d’extrémités d’arrivée situées sur le cercle C3.
AIDE pour construire la médiatrice d'un segment, cliquer sur le lien suivant :
Médiatrice d'un segment, puis appuyer 1 fois sur le bouton "play". Patience... L'image de 2 petits coeurs va apparaître, appuyer alors à nouveau sur le bouton "play".
Découpage et pliage :
- Découper sur les segments et les arcs de cercles rouges.
- Décorer la petite fleur. Pour écrire un petit mot et obtenir des traits ne bavant pas au contact de l’eau, utiliser les crayons à bille, sinon, utiliser la peinture ou les crayons feutres (méthode du lavis).
- Plier les pétales de la petite fleur sur le plus petit cercle C3 dans l’ordre et orientés vers le centre. Bien écraser les plis afin de casser légèrement les fibres du papier. Mettre de l’eau (de préférence tiède) dans un verre et poser la fleur sur la surface de l’eau comme un nénufar(2).
Surprise ! Magie ! La petite fleur de nénufar est en mouvement : elle s’ouvre toute seule !
Logiciel de géométrie dynamique en ligne :
 (Cliquer sur le logo du logiciel en ligne).
(Cliquer sur le logo du logiciel en ligne).
Fiche de la Math'@ctivité mouvement Petite fleur de nénufar à télécharger :
La fiche complète au format pdf :  .
.
Fiche de patrons à télécharger :
Des patrons de la Math'@ctivité mouvement Petite fleur de nénufar :  peuvent être téléchargés en cliquant sur cette image. Il ne restera plus qu'à imprimer la feuille, découper les patrons et les décorer en suivant les indications données ci-dessus, les plier, prendre un verre rempli d'eau et enfin déposer la petite fleur de nénufar.
peuvent être téléchargés en cliquant sur cette image. Il ne restera plus qu'à imprimer la feuille, découper les patrons et les décorer en suivant les indications données ci-dessus, les plier, prendre un verre rempli d'eau et enfin déposer la petite fleur de nénufar.
Et pour les plus "pressés", ci-après, d'autres patrons décorés (pour certains, recto-verso)... :
 .
.
 Math'@ctivités 3D : Infos ;
Math'@ctivités 3D : Infos ;
 Anamorphose Cylindrique ;
Anamorphose Cylindrique ;
 Ballon de Foot 1 ;
Ballon de Foot 1 ;
 Boîte de Kepler-Vasarely ;
Boîte de Kepler-Vasarely ;
 Boîte Rosace 3D ;
Boîte Rosace 3D ;
 Casse-tête polyèdre étoilé ;
Casse-tête polyèdre étoilé ;
 Chapeau du Bonheur ;
Chapeau du Bonheur ;
 Cœur tressé ;
Cœur tressé ;
 Dés solides de Platon ;
Dés solides de Platon ;
 Flexacube ;
Flexacube ;
 Flexagone ;
Flexagone ;
 Hexabelle de nuit ;
Hexabelle de nuit ;
 Kaléïdocycle d'ordre 6 ;
Kaléïdocycle d'ordre 6 ;
 Onglet marque-page ;
Onglet marque-page ;
 Planètorange ;
Planètorange ;
 Math'@ctivités mouvement : Infos
Math'@ctivités mouvement : Infos  Math'@ctivités 2D : Infos
Math'@ctivités 2D : Infos 


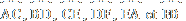 (il y en a 12) ;
(il y en a 12) ;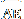 et C2 situé le plus au Sud) puis, dans l’ordre et dans le sens des aiguilles d’une montre, les points : N, O, P, Q, R, S, T, U, V, W et X ;
et C2 situé le plus au Sud) puis, dans l’ordre et dans le sens des aiguilles d’une montre, les points : N, O, P, Q, R, S, T, U, V, W et X ;





