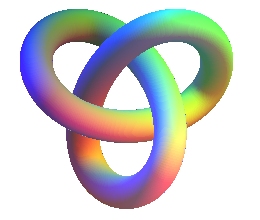Math'@ctivité 3D : Flexagone

(Les sommaires sont dans les onglets en haut de page et le '@' ci-dessus permet d'accéder à l'accueil du site)

Le résultat final est un anneau de moebius à la façon d'Escher et il est manipulable. Il se range dans une pochette d'origami lui servant de présentoir. Ce sont des objets en 3 dimensions (3D) même si le flexagone est applati lorsqu'il n'est pas manipulé. Pour voir le flexagone en action, cliquer sur l'animation ci-contre puis sur le bouton play.
Pour voir une autre animation vidéo, cliquer sur l'icône suivante ("V" comme vidéo) puis 2 fois sur le bouton "play" : .
Infos... Pourquoi ce nom flexagone ? :

Sa définition est précisée dans Wikipédia, une encyclopédie libre sur Internet :

"Le flexagone est un objet topologique issu du ruban de Moebius. Il existe plusieurs formes de flexagones mais la plus connue est le trihexaflexagone : un hexagone formé de [...] triangles équilatéraux pliés à partir d'une bande de papier. Le flexagone a été découvert par Arthur Stone en 1939, alors qu'il étudiait à Princeton. L'objet enthousiasma plusieurs personnes qui fondèrent un "Comité d'investigation chargé d'enquêter sur les propriétés du flexagone"." Extrait de http://fr.wikipedia.org/wiki/Flexagone. Le flexagone présenté dans cette page serait alors un trihexaflexagone.
Au 29/10/2007, il était précisé dans cette encyclopédie qu'un trihexaflexagone a 10 triangles équilatéraux or c'est une erreur puisque 9 suffisent pour obtenir ce type de flexagone. 3 hexagones composés de 6 trianges équilatéraux soient 3*6=18. Comme chaque triangle équilatéral a un verso et un recto, le trihexaflexagone a seulement 18:2=9 triangles équilatéraux. L'éventuel 10ème servant de languette.

Le trihexaflexagone est un anneau de Moebius à trois demi-torsions. Le bord d'un trihexaflexagone est un noeud de trèffle. Le flexagone est une représentation ludique d'une toute petite partie de la théorie des noeuds en mathématiques.

Le flexagone est une sorte de casse-tête puisqu'il a des faces cachées qui se dévoilent lorsqu'on le manipule.

Matériel nécessaire pour le flexagone et sa pochette-présentoir :
instruments de géométrie : règle graduée et compas ;

1 feuille A4 (grammage : environ 80g/m² ou 90g/m²) pour le flexagone ;

1 feuille A4 (grammage : environ 80g/m² ou 90g/m²) pour sa pochette-présentoir ;

colle à papier ;

ciseaux, crayon à papier et crayons de couleur ou peinture.

Programme de construction (savoirs et savoir-faire mathématiques : propriétés du triangle équilatéral et du triangle isocèle, médiatrice d’un segment, cercle circonscrit au triangle équilatéral, hexagone, et le vocabulaire géométrique correspondant : cercle, rayon, centre, point d’intersection, sommet, etc.) :

Construction du patron du flexagone :

- placer le point O₀ au milieu du côté gauche de la feuille A4 au format ‘paysage’ ;

- tracer la droite horizontale passant par O₀, la noter (d) ;

- construire c₀ le cercle de centre O₀ et de rayon 5 cm ;

- placer le point d’intersection entre la droite (d) et le cercle c₀, le noter O₁ ;

- construire c₁ le cercle de centre O₁ et de rayon O₁O₀ ;

- placer le 2ème point d’intersection entre la droite (d) et le cercle c₁, le noter O₂ ;

- construire c₂ le cercle de centre O₂ et de rayon O₁O₀ ;

- continuer de placer les points d’intersection et de construire les cercles jusqu’à c₅ et O₅ ;

- placer les points : A₁ point d'intersection 1 des cercles c₀ et c₁, B₁ point d'intersection 2 des cercles c₀ et c₁, …, jusqu’à B₅ point d'intersection 2 des cercles c₄ et c₅ ;

- tracer les hexagones : O₀A₁A₂O₂B₂B₁, O₁A₂A₃O₃B₃B₂, O₂A₃A₄O₄B₄B₃ et O₃A₄A₅O₅B₅B₄ ;

- tracer les segments : [O₀A₁], [O₁B₁], [O₄A₅] et [O₄B₅] ;

- ajouter une languette trapèze de base adjacente au segment [B₅O₅] (elle est en vert sur le patron affiché plus bas).

Programme de construction du motif du flexagone :

- construire le centre D₁ du cercle circonscrit au triangle O₀A₁O₁ et tracer les segments [D₁O₀], [D₁A₁] et [D₁O₁] ;

- refaire cette même dernière construction pour les 17 autres triangles ;

- colorier, avec les couleurs primaires, les triangles isocèles ainsi obtenus comme ci-dessous (les triangles isocèles O₀D₁O₁ et O₀D₁A₁ en rouge, O₁D₁A₁ laissé en blanc, etc.) :

Découpage, pliage, collage et assemblage :

Découper. Effacer les traits inutiles. Avec une pointe sèche de compas et une règle, repasser les segments du patron pour casser les fibres du papier. Plier en deux le long de l’axe (O₁O₂) et coller les triangles superposés sauf les deux situés à l’extrémité opposée à la languette qui sont à coller à la fin.

Plier les triangles équilatéraux à la manière d'un anneau de Moebius c'est-à-dire qu'une extrémité est assemblée à l'autre en la retournant. Surprise ! Les triangles isocèles d’une même couleur sont rassemblés sur une même face du flexagone. Il y 6 faces possibles. Il reste à manipuler le flexagone à la manière d’un anneau de Moebius.

Et si cela est difficile : regarder attentivement la vidéo et télécharger plus bas les fichiers au format pdf (imprimer 1 feuille du patron sur du papier A4 simple de 80g/m² ou 90g/m²). Le pliage de la pochette présentoire (à télécharger aussi) est présenté dans la vidéo jointe en cliquant sur l'icône suivante.

Logiciel de géométrie 2D en ligne :

(Cliquer sur le logo du logiciel en ligne souhaité).

Fiche de la Math'@ctivité 3D "flexagone" à télécharger :

La fiche complète au format pdf : .

Liens Internet :

Les Mathématiques magiques : Venez au pays des Mathématiques magiques malicieuses et... très sérieuses. Vous découvrirez des tours de magie interactifs, de la télépathie..., des énigmes, cours et exercices animés, des jeux, des puzzles magiques, des illusions géométriques animées, des paradoxes, de la géométrie et des pavages dynamiques, des opérations anciennes interactives, des trucs malins, des anecdotes historiques, et de très nombreuses animations flash, dans le grenier à malices mathématiques de Thérèse EVEILLEAU. Pour obtenir la page concernant le flexagone, cliquer sur le lien suivant : http://perso.orange.fr/therese.eveilleau/pages/truc_mat/textes/flexagone.htm.
Un site MAGNIFIQUE !!

Le site Kangourou des Mathématiques est un site de vente de documents et d'objets mathématiques qui au-delà de la vente d'un flexagone à construire, présente l'objet magique dans sa rubrique "flexagone".

Aleph est un site de casse-tête, enigmes et problèmes mathématiques, problèmes de Sam Loyd. Cette page est dédiée au flexagone

Mathematische Basteleien est un site allemand génial dédié à des curiosités mathématiques à construire dont cette page, en anglais, réservée aux flexagones.

Le site EighthSquare.com est un site, en anglais, où quelques pages sont dédiées aux flexagones mais ceux-ci ne sont pas des trihexaflexagones. L'une des pages concerne l'histoire du flexagone.

Dans son site, en anglais, Jill Britton propose un logiciel libre permettant d'insérer des photographies dans des trihexaflexagones à imprimer. Le patron n'est pas le même que celui de Math'@ctivité mais son pliage s'effectue sur le même principe : pliage en deux, puis en accordéon et enfin en anneau de Moebius.

Une définition du ruban de Moebius dans l'encyclopédie gratuite en ligne Wikipedia.

Une présentation de découverte du ruban de Moebius par l'expérimentation faite par un jeune.

Une présentation essentiellement mathématique du ruban de Möbius et des références au graveur M.C. Escher sont écrites par Robert Ferréol et ses co-auteurs.

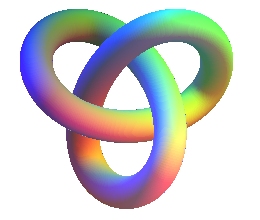Dans cette page de Robert Ferréol, il est question du noeud de trèfle. Le bord d'un trihexaflexagone en est un.

Un lien vers la page Notion sur la théorie des nœuds de la petite chronologie des maths de Serge Mehl.

Bienvenue sur Wikipédia, projet d’encyclopédie librement distribuable que chacun peut améliorer.

Pour obtenir des informations complémentaires sur une place possible de cette Math'@ctivité dans les programmes d'enseignement des mathématiques de l'Éducation Nationale Française ainsi que : des conseils pédagogiques (voire didactiques), des exercices et éléments de cours à différents niveaux de classes, d'autres programmes de construction, des fichiers à télécharger,etc., cliquer sur l'icône précédente puis accéder à mon 'Portail' Éducation et chercher dans la rubrique "Utilisation de Math'@ctivités dans l'enseignement", ou visiter les autres rubriques...

Des fichiers d'impression 3D et de découpe automatique ou laser sont disponibles sur mon site à l'adresse : http://www.art3d.fr.

Math'ctivité 3D

Flexagone