Math'@ctivité 2D : Trous d'aiguilles géométriques d'or

(Les sommaires sont dans les onglets en haut de page et le '@' ci-dessus permet d'accéder à l'accueil du site)

Trous d'aiguilles géométriques d'or

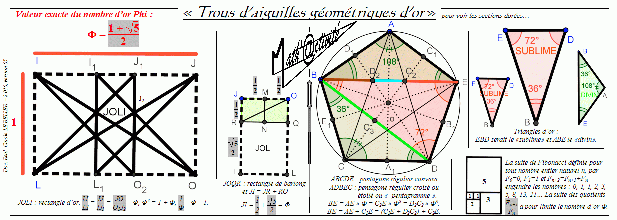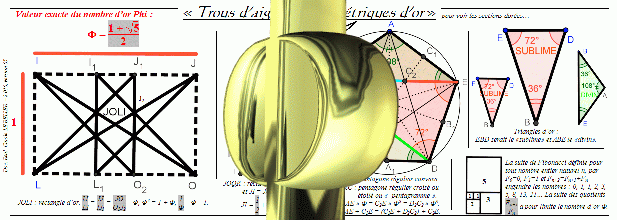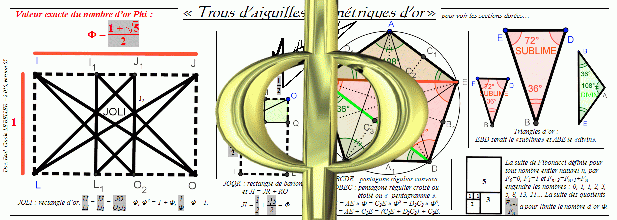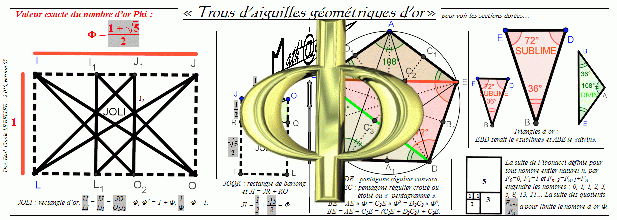
Les trous d'aiguilles géométriques d'or sont un outil pour voir des sections dorées dans des peintures ou des photographies de monuments. Je les classe dans les Math'@ctivité 2D.
La construction des figures d'or peut se faire à la main avec des instruments de géométrie traditionnels qui sont ici : la règle graduée, l'équerre, le rapporteur et le compas. Il faut ensuite les photocopier sur des feuilles transparentes.
Elle est plutôt conseillée à l'ordinateur, et entre autres, avec le logiciel de géométrie 2D : 'GeoGebra' (logiciel libre) ou 'geoplanW' (dont l'activX est gratuit ainsi que la version antérieure à celle de 2003), à imprimer directement sur un transparent.

Le résultat final est un outil pour voir des sections dorées dans des peintures ou des photographies de monuments. C'est un objet en 2 dimensions (2D).

Infos... Les trous d'aiguilles géométriques d'or, petite histoire :

"Ma collègue d’arts plastiques, professeure relais au Musée des beaux-arts de Rennes, m’a sollicitée pour travailler sur le nombre d’or dans des tableaux de l’exposition temporaire d’œuvres de Georges Folmer, artiste peintre (1895-1977). L’utilisation de la géométrie dynamique au service de l’art, ainsi que les liens entre mathématiques et ces œuvres, m’ont paru tout de suite évidents. Ensuite, j’ai eu deux entretiens (un lors du vernissage et l’autre par téléphone) avec Catherine Folmer-Santoni, la fille de Georges Folmer. Celle-ci m’a donné de précieux renseignements sur les activités de son père et sur des documents existants (publications).
J’ai commencé par rassembler mes documents, livres et fichiers sur Georges Folmer et sur le nombre d’or, puis j’ai mis à jour toutes mes informations à l’aide d’Internet. Et là..., j’ai eu l'idée, personnelle, d'inventer une math’@ctivité, le drôle d’outil : des « trous d’aiguilles géométriques d’or » pour « voir » des sections dorées…, et enfin, des activités et des animations sur le sujet, dont certaines utilisant la géométrie dynamique..

Matériel nécessaire :
un ordinateur, le logiciel GeoGebra et une imprimante ;

1 feuille feuille transparente pour imprimante ;

ciseaux.

Dossier à télécharger :

Le fichier permettant de construire les "trous d'aiguilles géométriques d'or" de la Math'@ctivité 2D ainsi qu'un parcours mathématique dans des oeuvres de Georges FOLMER (par contre sans les images). Cliquer sur l'image : .
Avec les images des oeuvres et quelques réponses, vous pouvez le télécharger à l'adresse du Site officiel de Georges FOLMER ci-après:

Liens Internet : mes incontournables...

..................... En lien préféré, forcément l'un de mes documents écrit pour le Musée des Beaux Arts de Rennes, et à télécharger sur le Site officiel de Georges FOLMER : Le nombre d'or et l'art.

------- Un lien tout particulier vers le Site des Amis de Georges FOLMER pour lui rendre hommage. Adresse : http://www.folmer.net/.

------- Une vidéo, et un interview de Catherine Folmer-Santoni (fille de l'artiste), portant sur l'exposition de Rennes consacrée à certaines oeuvres de Georges FOLMER. Adresse : http://culturebox.francetvinfo.fr/arts/expos/retrospective-georges-folmer-au-musee-des-beaux-arts-de-rennes-24661.

------- Article portant sur l'exposition à l’Organisation Mondiale de la Propriété Intellectuelle, OMPI, qui a accueilli en son siège à Genève certaines oeuvres de Georges FOLMER. Adresse : http://www.franceonugeneve.org/Exposition-Georges-Folmer.

------- Extrait de la revue publiée lors de l'exposition à l’Organisation Mondiale de la Propriété Intellectuelle, OMPI, qui a accueilli en son siège à Genève certaines oeuvres de Georges FOLMER. Adresse : http://beta.folmer.net/wp-content/uploads/2012/01/nombre_dor_geneve.pdf#pdfjs.action=download.

Math'ctivité 2D

Trous d'aiguilles géométriques d'or