Math'@ctivité 3D : Onglet marque-page

(Les sommaires sont dans les onglets en haut de page et le '@' ci-dessus permet d'accéder à l'accueil du site)

Le résultat final est une petite pochette faisant office d'onglet marque-page. C'est un objet en 3 dimensions (3D). Pour voir son utilisation, cliquer sur l'animation ci-contre puis sur le bouton play.

Infos... L'Onglet marque-page ?... :

L'onglet marque-page n'est constitué que d'un carré.
L’origami, loisir, stimulant intellectuel, outil éducatif, est aussi un symbole de paix.
La définition du l’"origami" est précisée dans Wikipédia, une encyclopédie libre sur Internet :
" L'origami (de oru, plier, et de kami, papier) est le nom japonais de l'art du pliage du papier. Cet art est originaire de la Chine entre le 1er et le IIe siècle, il est appelé jiezhi, terme qui regroupe les techniques de pliage de papier et de papier découpé […]. L'origami est un sujet d’étude pour les mathématiciens et aussi pour les enseignants de mathématiques, c’est la géométrie dans les doigts. "

Matériel nécessaire :
instruments de géométrie : règle graduée, équerre et compas ;

1 feuille A4 (grammage : environ 80g/m² ou moins) ;

colle à papier ;

ciseaux, crayon à papier et crayons de couleur ou peinture.

Programme de construction (savoirs et savoir-faire mathématiques : propriétés du carré et le vocabulaire géométrique correspondant, demi-droite, perpendiculaire et parallèle, arc de cercle avec son rayon et son centre, point d’intersection entre deux arcs de cercles, centre et sommets d’un carré, diagonales d’un carré, triangle isocèle rectangle en un sommet et sa base principale.) :

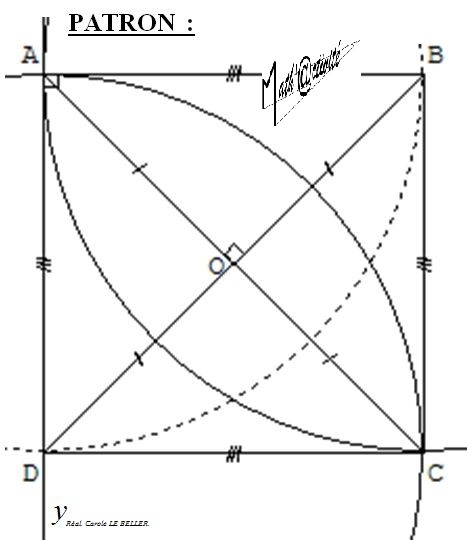
Construction du chapeau :

- tracer horizontalement un segment [AB] de longueur 14 cm ;

- à l’aide de l’équerre, construire une demi-droite [Ay) perpendiculaire à [AB] passant par A (y se situe au Sud de A) ;

- à l’aide du compas, reporter la longueur AB sur [Ay) et placer le point D tel que AD = AB (conserver l’écartement de compas);

- à l’aide du compas, tracer un arc de cercle de centre B et de rayon [BA] direction Sud (conserver l’écartement de compas) ;

- à l’aide du compas, tracer un arc de cercle de centre D et de rayon [BA] direction Est ;

- le point d’intersection entre ces deux arcs tracés est C ;

- tracer les segments [BC] et [CD] pour obtenir le carré ABCD ;

- tracer les deux diagonales du carré [AC] et [BD] (elles se croisent en leur milieu en formant un angle droit) ;

- placer le point d’intersection entre les diagonales et le nommer O. O est le centre du carré ABCD.

Et si cela est difficile : le télécharger, imprimer, décorer, découper, plier en suivant les indications ci-dessous, coller et consolider.

Découpage, pliage, et collage :

Découper le carré. Effectuer un « pli montagne » sur la diagonale [BD]. Les traits de construction se trouvent donc à l’extérieur, ils sont visibles et les sommets A et C sont superposés. Poser le triangle ABD isocèle rectangle en A face à vous sur sa base principale [BD]. (cf. : image 1)

Plier après avoir superposé le sommet A sur le centre O. Un petit carré avec l’une de ses diagonales parallèle à [BD] est alors visible. (cf. : image 2)

Plier après avoir superposé les sommets B et D sur le centre O. Les deux pliures sont parallèles au segment [AO]. Une sorte de pochette a été formée. Puis déplier. Les sommets B et D sont de nouveau à leur place d’origine. (cf. : images 3, 4 et 5)

Plier après avoir superposé les sommets B et C. Prendre le sommet B et le glisser dans la pochette. Il est superposé à O et est invisible de l’extérieur. Il permet de fixer un côté de la pochette sans avoir besoin de colle. (cf. : images 6 et 7)

De même, plier après avoir superposé les sommets D et C. Puis, prendre le sommet D et le glisser dans la pochette. Il est superposé à O et est invisible de l’extérieur. Il permet de fixer l’autre côté de la pochette sans avoir besoin de colle. (cf. : images 8 et 9)

Votre onglet marque-page est prêt à être fixé avec de la colle dans un cahier ou juste posé et utilisé comme un marque-page dans un livre.

Logiciel de géométrie 2D en ligne :

(Cliquer sur le logo du logiciel en ligne souhaité).

Fiche de la Math'@ctivité 3D Onlet marque-page à télécharger :

La fiche complète au format pdf : .

Fiches des patrons à télécharger :

Le patron de la Math'@ctivité 3D Onglet marque-page est constitué d'une seule pièce. Ci-après, en cliquant sur l'image, peuvent être téléchargés deux patrons en noir et blanc : . Il ne restera plus qu'à les mprimer, les décorer, les découper, passer les traits à la pointe sèche du compas, plier, assembler et coller en suivant les indications des images et de la vidéo ci-dessus.

Et pour les plus "pressés", ci-après, des patrons tous décorés... : . ,

Réalisations en images :

Pour voir des réalisations personnelles, en accédant à la rubrique Top10-Images, cliquer sur l'image suivante : .

Liens Internet :

Pour obtenir des informations complémentaires sur une place possible de cette Math'@ctivité dans les programmes d'enseignement des mathématiques de l'Éducation Nationale Française ainsi que : des conseils pédagogiques (voire didactiques), des exercices et éléments de cours à différents niveaux de classes, d'autres programmes de construction, des fichiers à télécharger,etc., cliquer sur l'icône précédente puis accéder à mon 'Portail' Éducation et chercher dans la rubrique "Utilisation de Math'@ctivités dans l'enseignement", ou visiter les autres rubriques...

Math'ctivité 3D

Onglet marque-page