Math'@ctivité 3D : Chapeau du bonheur

(Les sommaires sont dans les onglets en haut de page et le '@' ci-dessus permet d'accéder à l'accueil du site)

Le résultat final est un chapeau cylindrique. C'est un objet en 3 dimensions (3D). Pour voir le chapeau en vidéo, cliquer sur l'animation ci-contre puis sur le bouton play.

Infos... Le Chapeau du Bonheur ?... :

Ce chapeau est formé d'un cylindre de révolution et d'un bord de chapeau en forme de disque troué. Il est constitué de 5 pièces. Je l'ai appelé le "Chapeau du Bonheur" car il apportera à son possesseur autant de bonheur que 'pi' a de décimales...

Infos... Le chapeau du bonheur et 'pi' :

Le chapeau du Bonheur est un cylindre de révolution. Il est la réduction à l’échelle un tier d’un chapeau de 54 cm de tour de tête (périmètre P des petits disques, bases du cylindre) de hauteur h = 10,5 cm et de bord b = 6 cm. Calculs permettant de déterminer le rayon r du fond de chapeau : On a P égale le produit de 2 par r et par pi donc r égale 54 divisé par le produit de 2 par pi. Le résultat est r = 8,6 cm.
A l’échelle 1/3, on aura donc : h’ = h * 1/3 = 10,5 * 1/3 = 3,5 cm, b’ = b * 1/3 = 6 * 1/3 = 2 cm, r’ = (54/(2 * pi)) * 1/3 soit r' est environ égal à 2,9 cm et P’ = 54 * 1/3 = 54/3 = 18 cm.

Matériel nécessaire :
instruments de géométrie : règle graduée, équerre et compas ;

1 feuille A4 épaisse (grammage : environ 160g/m² ou plus) ;

colle à papier ;

ciseaux, crayon à papier et crayons de couleur ou peinture.

Programme de construction (savoirs et savoir-faire mathématiques : rectangle, triangle isocèle, cercle et disque, périmètre, rayon, cylindre de révolution, et le vocabulaire géométrique correspondant. Pour les calculs de longueurs, le nombre 'pi' noté a été utilisé.) :

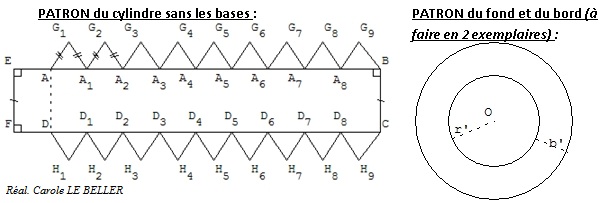
Construction du chapeau :

- positionner sa feuille A4 dans le sens ‘portrait’ ;

- à 2 cm du haut de la feuille et à partir du bord gauche de la feuille, construire un rectangle EBCF de longueur 18,2 cm et de largeur 3,5 cm ;

- placer le point A appartenant au segment [EB] tel que EA = 2 cm. Placer le point D appartenant au segment [FC] tel que FD = 2 cm ;

- à partir de A, construire des triangles isocèles de longueur de base principale 2 cm et de hauteur 1,5 cm. Les bases de ses triangles sont des segments de [AB], il y en a huit et le 9^ème n’est pas isocèle sa base mesure 2,2 cm. Faire une même série de triangles à partir de D ;

- construire deux cercles de rayon 5 cm puis deux autres cercles de rayon 3 cm à l’intérieur des précédents. Ces cercles s’appellent des cercles concentriques.

Et si cela est difficile : télécharger, imprimer, décorer, découper, plier en suivant les indications ci-dessous, coller et enfin assembler le chapeau.

Découpage, pliage, assemblage et collage :

Découper la forme composée du rectangle et des triangles. Avec une pointe sèche de compas et une règle, repasser les bases principales des triangles isocèles pour casser les fibres du papier. Coller la languette rectangulaire EADF de manière à former la face latérale d’un cylindre de révolution. Les languettes triangulaires du haut seront pliées vers l’intérieur du cylindre et celles du bas vers l’extérieur du cylindre.

Découper les deux grands disques puis les deux petits disques intérieurs sans altérer les grands disques alors troués.

Coller l’un des deux petits disques à l’intérieur du cylindre, les languettes triangulaires se trouvant au dessus du chapeau. C’est le fond du chapeau ou, en mathématiques, l’une des deux bases du cylindre de révolution. Coller le petit disque restant sur le haut du chapeau.

Enfiler le cylindre dans l’un des deux grands disques troués et le coller. C’est le bord du chapeau. Coller le grand disque troué restant à l’extérieur pour cacher les languettes triangulaire du bord du chapeau.

Le chapeau du Bonheur fini, il est possible d’y glisser dans le fond un petit cœur plié (cf. fiche Math’@ctivité 2D : ‘Cœur pliable en disque’).
Logiciel de géométrie 2D en ligne :

(Cliquer sur le logo du logiciel en ligne souhaité).

Fiche de la Math'@ctivité 3D Chapeau du Bonheur à télécharger :

La fiche complète au format pdf : .

Fiches des patrons à télécharger :

Le patron de la Math'@ctivité 3D Chapeau du onheur est constitué de 5 pièces. Ci-après, en cliquant sur l'une des images, peuvent être téléchargés le patron en noir et blanc : . Il ne restera plus qu'à l'imprimer, le décorer, le découper, passer les traits à la pointe sèche du compas, plier, assembler et coller en suivant les indications de la vidéo ci-dessus.
Et pour les plus "pressés", ci-après, des patrons tous décorés... : , , , , , , .

Réalisations en images :

Cliquer sur l'image suivante : .

Pour voir des réalisations personnelles, en accédant à la rubrique Top10-Images, cliquer sur l'image suivante : .

Liens Internet :

Pour obtenir des informations complémentaires sur une place possible de cette Math'@ctivité dans les programmes d'enseignement des mathématiques de l'Éducation Nationale Française ainsi que : des conseils pédagogiques (voire didactiques), des exercices et éléments de cours à différents niveaux de classes, d'autres programmes de construction, des fichiers à télécharger,etc., cliquer sur l'icône précédente puis accéder à mon 'Portail' Éducation et chercher dans la rubrique "Utilisation de Math'@ctivités dans l'enseignement", ou visiter les autres rubriques...

Des fichiers d'impression 3D et de découpe automatique ou laser sont disponibles sur mon site à l'adresse : http://www.art3d.fr.

Math'ctivité 3D

Chapeau du bonheur