Math'@ctivité 3D : Planètorange

(Les sommaires sont dans les onglets en haut de page et le '@' ci-dessus permet d'accéder à l'accueil du site)

Le résultat final est une sorte de 'sphère'. C'est un objet en 3 dimensions (3D). Pour voir le Planètorange 'rouler', cliquer sur l'animation ci-contre puis sur le bouton play.

Infos... Pourquoi ce nom Planètorange ? :

Ce nom a été une idée commune entre Corinne Le Quellenec en 2000 et moi. Vous l'avez deviné, cette math'@ctivité ressemble à une planète et à une orange en demi-quartiers. Nous aurions pu aussi lui donner un nom lié à la sphère ou à la boule mais cela faisait presque trop 'mathématique'. C'est Corinne qui connaissait la construction et les mesures précisées ci-dessous. J'ai écrit le programme de construction du patron et j'ai réalisé la fiche et les modèles avec geoplanW (fichiers : pdf joints en bas de page et g2w en téléchargement dans la rubrique 'Enseignement') chez moi sur mes temps de loisirs.

Infos... La sphère, la géosphère et la boule

"Une sphère est une surface à 3 dimensions dont tous les points sont situés à une même distance d'un point appelé centre. La valeur de cette distance commune au centre est appelée le rayon de la sphère. Elle n'inclut donc pas les points situés à une distance inférieure au rayon, au contraire de la boule. Concrètement, on peut voir une sphère comme une coquille vide infiniment mince.
Une sphère approximative est appelée géosphère en référence à la Terre dont la surface n'est pas une sphère parfaite.[...] Dans un espace euclidien, il s'agit du ballon que tout le monde associe au terme de sphère. Dans un espace non-euclidien ou dans le cas de la définition d'une distance non euclidienne, la forme peut être plus complexe.[...]
Une boule est l'ensemble des points d'un espace dont la distance à un point - appelé centre - est, au plus, égale à un nombre réel positif donné. Ce nombre est appelé le rayon de la boule. La boule, en mathématiques, est un sous-ensemble particulier d'un espace métrique. Dans un espace non-euclidien ou dans le cas de la définition d'une distance non euclidienne, sa forme n'est pas nécessairement ronde. Une boule peut être également définie comme le volume formé par la rotation d'un disque autour de son diamètre. " Extrait de hhttp://fr.wikipedia.org/wiki/Sphère.

Le Planètorange est constitué de disques avec quelques défaux... Il pourrait être une 'géoboule'... Mais ce terme n'existe pas...

Matériel nécessaire :
instruments de géométrie : règle graduée, rapporteur ou compas, et équerre ;

1 feuille A4 épaisse (grammage : environ 160g/m² ou plus) ;

ciseaux, crayon à papier et crayons de couleur ou peinture.

Programme de construction (savoirs et savoir-faire mathématiques : Cercle, angles, segments perpendiculaires, milieux et constructions. Utilisation des fractions : fractions et partages, un nombre multiplié par une fraction.) :

Construction de 2 disques identiques D1 et D2 :

- Tracer un cercle C de centre O et de diamètre 70 mm. On obtient le disque D1.
- Partager le disque D1 en 6 parts égales en utilisant le rapporteur ou le compas.
- Placer les points du cercle C aux extrémités de chaque part. Les nommer A1, A2, A3, A4, A5 et A6.
- Tracer les segments [OA1], [OA2], [OA3], [OA4], [OA5] et [OA6] si ce n’est pas déjà fait.
- Tracer un cercle C1 de centre O et de diamètre du diamètre de C.
- Placer les 6 points d’intersections du cercle C1 et des segments [OA1], [OA2], [OA3], [OA4], [OA5] et [OA6]. Ils seront nommés respectivement B1, B2, B3, B4, B5 et B6.
- Repasser en gras les segments [A1B1], [A2, B2], [A3, B3], [A4B4], [A5, B5] et [A6, B6].

Reproduire cette construction 1 fois afin d’avoir deux disques identiques, nommés D1 et D2.

Construction du disque D3 :

- De la même manière, construire un cercle de diamètre 80 mm.
- Le cercle à l’intérieur sera de diamètre du diamètre du cercle déjà construit. Le disque obtenu sera nommé D3.

Construction de 3 disques identiques D4, D5 et D6 :

- Construire un cercle C4 de diamètre 80 mm et de centre O4. Tracer un segment [QR], un diamètre de C4.
- Construire les milieux M1 et M2 des segments [QO4] et [O4R] respectivement.
- Tracer en gras 3 segments, mesurant chacun 20 mm, perpendiculaires à [QR] dont les milieux sont M1, O4 et M2 respectivement.

Reproduire cette construction deux autres fois afin d’obtenir trois disques identiques D4, D5 et D6.

Il peut exister d'autres programmes de construction (voir mon 'Portail' ).

Et si cela est difficile : télécharger, imprimer, décorer, découper, assembler en suivant les indications ci-dessous et enfin le planètorange pourra rouler.

Découpage et assemblage :

Découper les 6 disques et les fentes selon les segments repasser en gras. A partir de D4, D5 et D6, il est obtenu 6 demi-disques.

Effacer les traits inutiles. On peut décorer – à plat – les surfaces visibles.

Assembler en partant d’un demi-disque, emboîter D3 dans la fente du centre puis D1 et D2 au-dessus et en dessous de D3. Emboîter les 5 autres demi-disques.

Logiciel de géométrie 2D en ligne :

(Cliquer sur le logo du logiciel en ligne souhaité).

Fiche de la Math'@ctivité 3D Planètorange à télécharger :

La fiche complète au format pdf : .

Fiches des patrons à télécharger :

Le patron complet de la Math'@ctivité 3D Planètorange avec le codage : ou sans le codage : 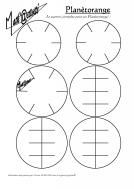, peut être téléchargé en cliquant sur l'une de ses images. Il ne restera plus qu'à l'imprimer, le décorer, le découper, l'assembler en suivant les indications ci-dessus et enfin vous pourrez faire rouler le planètorange.
Et pour les plus "pressés", ci-après, des patrons décorés... : 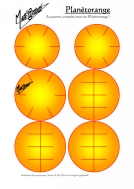, . Conseil : vous pouvez imprimer au verso l'un des dégradés de couleurs ci-après afin de ne pas avoir de faces blanches : , .

Réalisations en images :

Pour voir des réalisations personnelles, en accédant à la rubrique Top10-Images, cliquer sur l'image suivante : ..

Lien Internet :

Le Site MathsGéo fait un tour d'horizon (mathématiques) sur la sphère : définition, propriétés, sections planes, etc.

Bienvenue sur Wikipédia, projet d’encyclopédie librement distribuable que chacun peut améliorer.

Pour obtenir des informations complémentaires sur une place possible de cette Math'@ctivité dans les programmes d'enseignement des mathématiques de l'Éducation Nationale Française ainsi que : des conseils pédagogiques (voire didactiques), des exercices et éléments de cours à différents niveaux de classes, d'autres programmes de construction, des fichiers à télécharger,etc., cliquer sur l'icône précédente puis accéder à mon 'Portail' Éducation et chercher dans la rubrique "Utilisation de Math'@ctivités dans l'enseignement", ou visiter les autres rubriques...

Des fichiers d'impression 3D et de découpe automatique ou laser sont disponibles sur mon site à l'adresse : http://www.art3d.fr.

Math'ctivité 3D

Planètorange